| Home |
Mechatronics |
About RMS |
DMC Sub |
Audio Design |
Education |
Kits & Parts |
Automatic current bias circuit
- Introduction
- Power supply
- Signal path
- Automatic current bias circuit
- Computer Modelling
- Measurements
The automatic current bias circuit is based on the circuit that is introduced by Menno van der Veen in his book: "High-end Valve amplifiers 2" (in English; ISBN 978-0-905705-90-3).
The circuit of Menno van der Veen utilises a comparator to measure the voltage level over the cathode series resistor. The circuit effectively controls the duty-cycle of the resulting squarewave signal. This duty-cycle is constant at different signal levels. The circuits works fine and Menno claims that the switching of the comparator is not perceivable in the audio signal but I liked to even avoid any hard switching and designed a modified circuit.
Before introducing the modified circuit first the problem of autobias is explained with a simplified drawing, showing the cathode current over time of one of the power tubes at different signal levels. The bias current is set at 50 mA and the tubes are assumed ideally linear over its current range. The current through the power tubes can however never become negative and this is the main cause of the problem.

A class A-B amplifier behaves like a class A (both powertubes with mutually inverted identical signal over the full waveform), amplifier at low signal levels and gradually becomes class B (positive and negative signal voltages separated over the two power tubes) at higher signal levels. This means that with 50mA bias current an AC signal with 50 mA amplitude (blue curve) will result in a current through both tubes ranging from 0-100 mA (50+/-50 mA) for the first tube and 100-0 mA for the second tube. Below 50 mA amplitude (green curve) the system is always proportional over the full signal period and behaves as class A. Above 50 mA amplitude the signal clips at 0 mA and the second tube has to compensate for that effect. In reality the transition is less sharp and the resulting nonlinearity (cross-over distortion) can be kept at a reasonable low level.
When controlling the bias current one has to determine the actual value out of the measured total cathode current for each tube. With low signal levels this is easy to accomplish as it equals the average current level which is obtainable by adding a low-pass filter. At elevated signal levels such a simple filter would give erroneous results due to the clipping. The average signal level would increase (no negative values) and consequently the controller will reduce the bias current to keep the average value of the current constant until the bias current part has become zero, resulting in severe cross-over distortion.
The above drawing also indicates the output of a comparator switching around 50 mA. The resulting squarewave (black lines) will have a constant duty-cycle of 50% when the bias current is equal to 50 mA, independent of the signal level. With different bias-current levels the duty-cycle will no longer be equal to 50% so it can be used to control the bias current like Menno van der Veen has done.
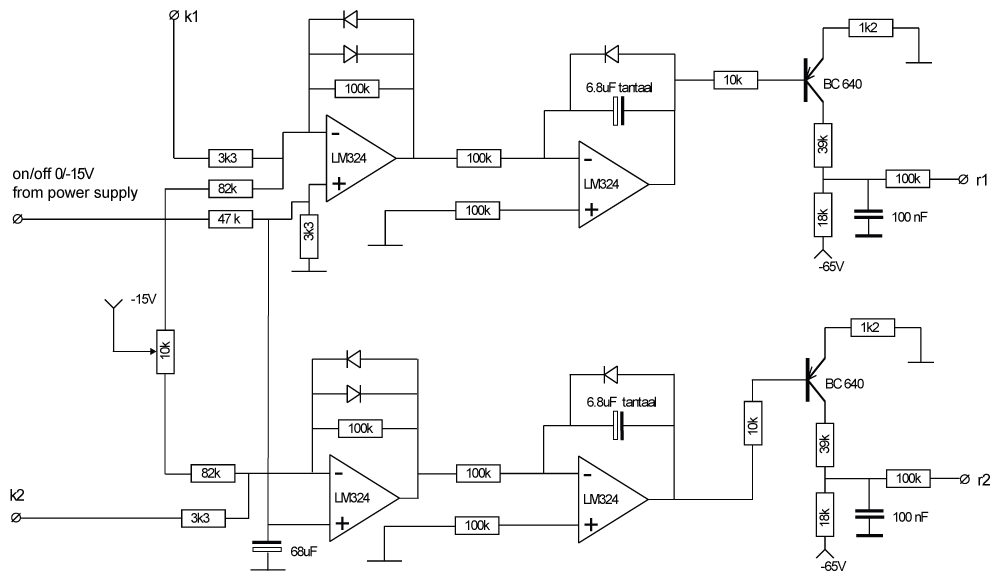
The circuit below is a modification that combines both systems. At low signal levels the circuit behaves like a simple low-pass filter and at high signal levels it creates a squarewave of which the duty-cycle is controlled. as a result no hard switching occurs at low signal levels and gradually harder switching occurs at elevated signal levels, where any related noise will not be perceivable anymore.
First the basic working principle at low signal levels for the upper half of the circuit is explained. The lower half has an identical functionality for the other tube. The current level is set by a negative voltage of 15V over the resistors of 82k to the inverting input of the first Op-Amp. The inverting input is normally equal to the non-inverting input (= 0V). This means that the average cathode voltage k1 over the 3k3 resistors should compensate the current over the 82k resistors to give average zero control voltage out of the Op-Amp. The second Op-Amp acts as an inverting integrator (low-pass starting at 0Hz) and its output controls the voltage over the base of the BC640 transistor that controls the negative bias voltage. A higher average voltage over k1 than the setpoint creates an average negative output voltage of the first Op-Amp. This gives a rising voltage at the output of the inverting integrator. As a result the transistor will conduct less current and the negative gate bias voltage r1 will increase, resulting in its turn in a reduction of the bias current.
At higher signal levels the diodes over the 100k resistor of the first Op-Amp will result in a similar squarewave as shown in the drawing and the integrator will now react on the duty cycle, being the average voltage level around zero of the squarewave.
Some additional parts need further clarification:
- The potentiometer at the setpoint is used to set equal levels for the bias current of both tubes as differences can occur due to component tolerances. This setting must be very precise because a ring-core transformer is easily saturated with different bias current levels. The magnetic field contributions in the core by both currents work opposite to each other).
- At starting up, before the high voltage to the tubes is applied, the power supply feeds a voltage of -15V to the non-inverting inputs of the first Op-Amps via a 47k resistor, attenuated by a 3k3 resistor parallel to a 68 μF capacitor, to filter out noise. The negative voltage at the non-inverting input forces the output of the Op-Amp negative, giving an increase of the integrator output voltage, shutting the transistor off. As a result the maximum level of negative bias voltage is supplied as a starting point for the bias control. In this way overcurrent through the power tubes is avoided.
- The diode over the integrator capacitor is used to prevent negative voltages over the electrolytic capacitor. Under normal operating conditions this voltage is always positive.
- The integrator time constant is 0.68 sec so higher frequency signals will be transferred less to the bias voltage. Still this is a proportional feedback circuit with impact on the LF behaviour and this impact is examined in the computer modelling section.